
在运动控制中,精度(Accuracy)也称绝对精度,是指在特定维度下到达指令位置的准确性。通常需要测量全行程内多点的误差,统计上使用P-V、P-P或3σ统计方式作为考量。
绝对精度和重复精度
提高绝对精度是一项十分困难且成本高昂的工作,但提高重复定位精度,并在控制器层面进行合理应用,是一种高效且常见的方法。

图1绝对精度和重复精度
二维精度通常指运动平台在X轴和Y轴两个坐标系中的准确性和稳定性。它取决于运动平台自身的机械性能、反馈系统和驱动系统。要测量二维绝对精度数据,需要使用更可靠的二维量测方法。尽管驱控系统可以提供直观的二维反馈数据,但反馈数据和精度是两个不同的概念。
下图用X和Y坐标轴的偏差来表示二维精度。

图2 二维误差
二维误差的来源
组成X轴和Y轴各自定位误差(重复定位精度)是二维精度最容易理解的来源。然而,二维精度的产生远大于此。X轴和Y轴的垂直性对二维误差的大小上起着至关重要的作用;同时,X轴和Y轴的直线度也会影响到垂直轴的定位精度;每个轴的偏摆、俯仰、翻滚误差不仅影响定位,还会带来阿贝误差,进而影响最终的定位精度。为了简化从两个一维轴性能到二维误差的推导过程,我们需要应用困难的理论公式。

图3 二维误差部分来源分析
若要实现良好的定位,一种方式是采用精度更高的位置反馈进行位置闭环运算,但这种方式成本高且难度极大;另一种相对经济可行的方式是使用精确的测量方法来测试可重复的二维误差,并在运动控制器中进行实时位置补偿。
雅科贝思二维补偿
雅科贝思提供多种二维补偿的驱控方案,运动控制器的二维补偿方案在雅科贝思已经得到了实际验证。
第二代补偿方式操作简便、稳定可靠,并且通过一次差值的方式在中间位置基本满足了大多数二维补偿的应用需求。
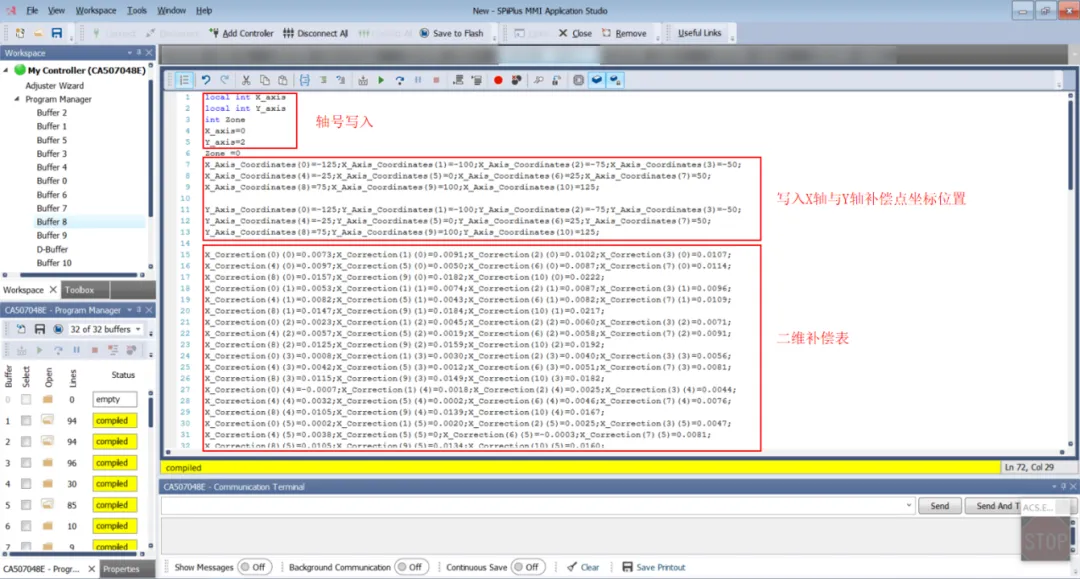
图4 二维补偿程序前段

图5 二维补偿程序后段
二维误差标定
对于二维误差的标定,核心是使用二维精度更高的反馈或样品进行坐标标定。使用二维编码器反馈是一种成本相对较高的方案,其核心是高精度的二维光栅,且大面型的反馈也很难找到。除了机床应用外,HEIDEHAIN提供的KGM平面光栅系统也可用于精密平台误差标定。

图6 平面光栅(来自海德汉)
另外,通过使用其他高精度标定板并结合相机,也可以实现误差值的标定。根据标定点数量不同,标定出二维点阵的位置误差,并写入补偿表中,从而实现动态补偿。

图7 标定板标定二维精度
综上所述,雅科贝思提供高精度运动平台,并为客户提供精确的定位解决方案。无论在半导体、光学、检测等领域,我们都秉承以客户需求为中心,为客户提供满意的高精度定位解决方案。
